A post about simulating data from a generalized linear mixed model (GLMM), the fourth post in my simulations series involving linear models, is long overdue. I settled on a binomial example based on a binomial GLMM with a logit link.

I find binomial models the most difficult to grok, primarily because the model is on the scale of log odds, inference is based on odds, but the response variable is a counted proportion. I use the term counted proportion to indicate that the proportions are based on discrete counts, the total number of “successes” divided by the total number of trials. A different distribution (possibly beta) would be needed for continuous proportions like, e.g., total leaf area with lesions.

Models based on single parameter distributions like the binomial can be overdispersed or underdispersed, where the variance in the data is bigger or smaller, respectively, than the variance defined by the binomial distribution. Given this, I thought exploring estimates of dispersion based on simulated data that we know comes from a binomial distribution would be interesting.

I will be simulating data “manually”. However, also see the simulate() function from package lme4. I find this function particularly useful if I want to simulate data based on a fitted model, but it can also be used in situations where you don’t already have a model.

R packages

I’ll be fitting binomial GLMM with lme4. I use purrr for looping and ggplot2 for plotting results.

library(lme4) # v. 1.1-23
library(purrr) # v. 0.3.4
library(ggplot2) # v. 3.3.2

The statistical model

As usual, I’ll start by writing out the statistical model using mathematical equations. If these aren’t helpful to you, jump down to the code. You may find that writing the code first and coming back to look at the statistical model later is helpful.

The imaginary study design that is the basis of my model has two different sizes of study units. This is a field experiment scenario, where multiple sites within a region are selected and then two plots within each site are randomly placed and a treatment assigned (“treatment” or “control”). You can think of “sites” as a blocking variable. The number of surviving plants from some known total number planted at an earlier time point is measured in each plot.

I first define a response variable that comes from the binomial distribution. (If you haven’t seen this style of statistical model before, my Poisson GLM post goes into slightly more detail.)

\[y_t \thicksim Binomial(p_t, m_t)\]

  • \(y_t\) is the observed number of surviving plants from the total \(m_t\) planted for the \(t\)th plot.
  • \(p_t\) is the unobserved true mean (proportion) of the binomial distribution for the \(t\)th plot.
  • \(m_t\) is the total number of plants originally planted, also know as the total number of trials or the binomial sample size. The binomial sample size can be the same for all plots (likely for experimental data) or vary among plots (more common for observational data).

We assume that the relationship between the mean of the response and explanatory variables is linear on the logit scale so I use a logit link function when writing out the linear predictor. The logit is the same as the log odds; i.e., \(logit(p)\) is the same as \(log(\frac{p}{1-p})\).

The model I define here has a categorical fixed effect with only two levels.

\[logit(p_t) = \beta_0 + \beta_1*I_{(treatment_t=\textit{treatment})} + (b_s)_t\]

  • \(\beta_0\) is the log odds of survival when the treatment is control.
  • \(\beta_1\) is the difference in log odds of survival between the two treatments, treatment minus control.
  • The indicator variable, \(I_{(treatment_t=\textit{treatment})}\), is 1 when the treatment is treatment and 0 otherwise.
  • \(b_s\) is the (random) effect of the \(s\)th site on the log odds of survival. \(s\) goes from 1 to the total number of sites sampled. The site-level random effects are assumed to come from an iid normal distribution with a mean of 0 and some shared, site-level variance, \(\sigma^2_s\): \(b_s \thicksim N(0, \sigma^2_s)\).

If you are newer to generalized linear mixed models you might want to take a moment and note of the absence of epsilon in the linear predictor.

A single simulation for a binomial GLMM

Below is what the dataset I will create via simulation looks like. I have a variable to represent the sites (site) and plots (plot) as well as one for the treatments the plot was assigned to (treatment). In addition, y is the total number of surviving plants, and num_samp is the total number originally planted (50 for all plots in this case).

Note that y/num_samp is the proportion of plants that survived, which is what we are interested in. In binomial models in R you often use the number of successes and the number of failures (total trials minus the number of successes) as the response variable instead of the actual observed proportion.

# # A tibble: 20 x 5
#    site  plot  treatment num_samp     y
#    <chr> <chr> <chr>        <dbl> <int>
#  1 A     A.1   treatment       50    40
#  2 A     A.2   control         50    26
#  3 B     B.1   treatment       50    42
#  4 B     B.2   control         50    23
#  5 C     C.1   treatment       50    48
#  6 C     C.2   control         50    33
#  7 D     D.1   treatment       50    28
#  8 D     D.2   control         50    19
#  9 E     E.1   treatment       50    45
# 10 E     E.2   control         50    35
# 11 F     F.1   treatment       50    45
# 12 F     F.2   control         50    25
# 13 G     G.1   treatment       50    35
# 14 G     G.2   control         50    21
# 15 H     H.1   treatment       50    42
# 16 H     H.2   control         50    26
# 17 I     I.1   treatment       50    47
# 18 I     I.2   control         50    30
# 19 J     J.1   treatment       50    42
# 20 J     J.2   control         50    31

I’ll start the simulation by setting the seed so the results can be exactly reproduced. I always do this for testing my methodology prior to performing many simulations.

set.seed(16)

Defining the difference in treatments

I need to define the “truth” in the simulation by setting all the parameters in the statistical model to values of my choosing. I found it a little hard to figure out what the difference between treatments would be on the scale of the log odds, so I thought it worthwhile to discuss my process here.

I realized it was easier to for me to think about the results in this case in terms of proportions of each treatment and then use those to convert differences between treatments to log odds. I started out by thinking about what I would expect the surviving proportion of plants to be in the control group. I decided I’d expect half to survive, 0.5. The treatment, if effective, needs to improve survival substantially to be cost effective. I decided that treatment group should have at least 85% survival (0.85).

The estimate difference from the model will be expressed as odds, so I calculated the odds and then the difference in odds as an odds ratio based on my chosen proportions per group.

codds = .5/(1 - .5)
todds = .85/(1 - .85)
todds/codds
# [1] 5.666667

Since the model is linear on the scale of log odds I took the log of the odds ratio above to figure out the additive difference between treatments on the model scale.

log(todds/codds)
# [1] 1.734601

I also need the log odds for the control group, since that is what the intercept, \(\beta_0\), represents in my statistical model.

log(codds)
# [1] 0

Here are the values I’ll use for the “truth” today:

  • The true log odds for on the control group, \(\beta_0\), will be 0
  • The difference in log odds of the treatment compared to the control, \(\beta_1\), will be 1.735.
  • The site-level variance (\(\sigma^2_s\)) will be set at 0.5.

I’ll define the number of sites to 10 while I’m at it. Since I’m working with only 2 treatments, there will be 2 plots per site. The total number of plots (and so observations) is the number of sites times the number of plots per site: 10*2 = 20.

b0 = 0
b1 = 1.735
site_var = 0.5
n_sites = 10

Creating the study design variables

Without discussing the code, since I’ve gone over code like this in detail in earlier posts, I will create variables based on the study design, site, plot, and treatment, using rep(). I’m careful to line things up so there are two unique plots in each site, one for each treatment. I don’t technically need the plot variable for the analysis I’m going to do, but I create it to keep myself organized (and to mimic a real dataset 😁).

site = rep(LETTERS[1:n_sites], each = 2)
plot = paste(site, rep(1:2, times = n_sites), sep = "." )
treatment = rep( c("treatment", "control"), times = n_sites)
dat = data.frame(site, plot, treatment)
dat
#    site plot treatment
# 1     A  A.1 treatment
# 2     A  A.2   control
# 3     B  B.1 treatment
# 4     B  B.2   control
# 5     C  C.1 treatment
# 6     C  C.2   control
# 7     D  D.1 treatment
# 8     D  D.2   control
# 9     E  E.1 treatment
# 10    E  E.2   control
# 11    F  F.1 treatment
# 12    F  F.2   control
# 13    G  G.1 treatment
# 14    G  G.2   control
# 15    H  H.1 treatment
# 16    H  H.2   control
# 17    I  I.1 treatment
# 18    I  I.2   control
# 19    J  J.1 treatment
# 20    J  J.2   control

Simulate the random effect

Next I will simulate the site-level random effects. I defined these as \(b_s \thicksim N(0, \sigma^2_s)\), so will randomly draw from a normal distribution with a mean of 0 and a variance of 0.5. Remember that rnorm() in R uses standard deviation, not variance, so I use the square root of site_var.

Since I am have 10 sites I draw 10 values, with each value repeated for each plot present within the site.

( site_eff = rep( rnorm(n = n_sites, 
                        mean = 0, 
                        sd = sqrt(site_var) ), 
                  each = 2) )
#  [1]  0.33687514  0.33687514 -0.08865705 -0.08865705  0.77514191  0.77514191
#  [7] -1.02122414 -1.02122414  0.81163788  0.81163788 -0.33121733 -0.33121733
# [13] -0.71131449 -0.71131449  0.04494560  0.04494560  0.72476507  0.72476507
# [19]  0.40527261  0.40527261

Calculate log odds

I now have fixed values for all parameters, the variable treatment to create the indicator variable, and the simulated effects of sites drawn from the defined distribution. That’s all the pieces I need to calculate the true log odds.

The statistical model

\[logit(p_t) = \beta_0 + \beta_1*I_{(treatment_t=\textit{treatment})} + (b_s)_t\]

is my guide for how to combine these pieces to calculate the log odds, \(logit(p_t)\).

( log_odds = with(dat, b0 + b1*(treatment == "treatment") + site_eff ) )
#  [1]  2.07187514  0.33687514  1.64634295 -0.08865705  2.51014191  0.77514191
#  [7]  0.71377586 -1.02122414  2.54663788  0.81163788  1.40378267 -0.33121733
# [13]  1.02368551 -0.71131449  1.77994560  0.04494560  2.45976507  0.72476507
# [19]  2.14027261  0.40527261

Convert log odds to proportions

I’m getting close to pulling values from the binomial distribution to get my response variable. Remember that I defined \(y_t\) as: \[y_t \thicksim Binomial(p_t, m_t)\] Right now I’ve gotten to the point where I have \(logit(p_t)\). To get the true proportions, \(p_t\), I need to inverse-logit the log odds. In R, function plogis() performs the inverse logit.

( prop = plogis(log_odds) )
#  [1] 0.8881394 0.5834313 0.8383962 0.4778502 0.9248498 0.6846321 0.6712349
#  [8] 0.2647890 0.9273473 0.6924584 0.8027835 0.4179445 0.7356899 0.3293085
# [15] 0.8556901 0.5112345 0.9212726 0.6736555 0.8947563 0.5999538

I can’t forget about \(m_t\). I need to know the binomial sample size for each plot before I can calculate the number of successes based on the total number of trials from the binomial distribution. Since my imaginary study is an experiment I will set this as 50 for every plot.

dat$num_samp = 50

I’ve been in situations where I wanted the binomial sample size to vary per observation. In that case, you may find sample() useful, using the range of binomial sample sizes you are interested in as the first argument.

Here’s an example of what that code could look like, allowing the binomial sample size to vary from 40 and 50 for every plot. (Code not run.)

num_samp = sample(40:50, size = 20, replace = TRUE)

Generate the response variable

Now that I have a vector of proportions and have set the binomial sample size per plot, I can calculate the number of successes for each true proportion and binomial sample size based on the binomial distribution. I do this via rbinom().

It is this step where we add the “binomial errors” to the proportions to generate a response variable. The variation for each simulated y value is based on the binomial variance.

The next bit of code is directly based on the distribution defined in the statistical model: \(y_t \thicksim Binomial(p_t, m_t)\). I randomly draw 20 values from the binomial distribution, one for each of the 20 proportions stored in prop. I define the binomial sample size in the size argument.

( dat$y = rbinom(n = n_sites*2, size = dat$num_samp, prob = prop) )
#  [1] 40 26 42 23 48 33 28 19 45 35 45 25 35 21 42 26 47 30 42 31

Fit a model

It’s time for model fitting! I can now fit a binomial generalized linear mixed model with a logit link using, e.g., the glmer() function from package lme4.

mod = glmer(cbind(y, num_samp - y) ~ treatment + (1|site), 
            data = dat,
            family = binomial(link = "logit") )
mod
# Generalized linear mixed model fit by maximum likelihood (Laplace
#   Approximation) [glmerMod]
#  Family: binomial  ( logit )
# Formula: cbind(y, num_samp - y) ~ treatment + (1 | site)
#    Data: dat
#      AIC      BIC   logLik deviance df.resid 
# 122.6154 125.6025 -58.3077 116.6154       17 
# Random effects:
#  Groups Name        Std.Dev.
#  site   (Intercept) 0.4719  
# Number of obs: 20, groups:  site, 10
# Fixed Effects:
#        (Intercept)  treatmenttreatment  
#             0.1576              1.4859

Make a function for the simulation

A single simulation can help us understand the statistical model, but usually the goal of a simulation is to see how the model behaves over the long run. To that end I’ll make my simulation process into a function.

In my function I’m going to set all the arguments to the parameter values as I defined them earlier. I allow some flexibility, though, so the argument values can be changed if I want to explore the simulation with, say, a different number of replications or different parameter values. I do not allow the number of plots to vary in this particular function, since I’m hard-coding in two treatments.

This function returns a generalized linear mixed model fit with glmer().

bin_glmm_fun = function(n_sites = 10,
                        b0 = 0,
                        b1 = 1.735,
                        num_samp = 50,
                        site_var = 0.5) {
     site = rep(LETTERS[1:n_sites], each = 2)
     plot = paste(site, rep(1:2, times = n_sites), sep = "." )
     treatment = rep( c("treatment", "control"), times = n_sites)
     dat = data.frame(site, plot, treatment)           
     
     site_eff = rep( rnorm(n = n_sites, mean = 0, sd = sqrt(site_var) ), each = 2)
     
     log_odds = with(dat, b0 + b1*(treatment == "treatment") + site_eff)
     prop = plogis(log_odds)
     dat$num_samp = num_samp
     dat$y = rbinom(n = n_sites*2, size = num_samp, prob = prop)
     
     glmer(cbind(y, num_samp - y) ~ treatment + (1|site),
           data = dat,
           family = binomial(link = "logit") )
}

I test the function, using the same seed, to make sure things are working as expected and that I get the same results as above. I do, and everything looks good.

set.seed(16)
bin_glmm_fun()
# Generalized linear mixed model fit by maximum likelihood (Laplace
#   Approximation) [glmerMod]
#  Family: binomial  ( logit )
# Formula: cbind(y, num_samp - y) ~ treatment + (1 | site)
#    Data: dat
#      AIC      BIC   logLik deviance df.resid 
# 122.6154 125.6025 -58.3077 116.6154       17 
# Random effects:
#  Groups Name        Std.Dev.
#  site   (Intercept) 0.4719  
# Number of obs: 20, groups:  site, 10
# Fixed Effects:
#        (Intercept)  treatmenttreatment  
#             0.1576              1.4859

Repeat the simulation many times

Now that I have a working function to simulate data and fit the model it’s time to do the simulation many times. The model from each individual simulation is saved to allow exploration of long run model performance.

This is a task for replicate(), which repeatedly calls a function and saves the output. When using simplify = FALSE the output is a list, which is convenient for going through to extract elements from the models later. I’ll re-run the simulation 1000 times. This could take awhile to run for complex models with many terms.

I print the output of the 100th list element so you can see the list is filled with models.

sims = replicate(1000, bin_glmm_fun(), simplify = FALSE )
sims[[100]]
# Generalized linear mixed model fit by maximum likelihood (Laplace
#   Approximation) [glmerMod]
#  Family: binomial  ( logit )
# Formula: cbind(y, num_samp - y) ~ treatment + (1 | site)
#    Data: dat
#      AIC      BIC   logLik deviance df.resid 
# 122.1738 125.1610 -58.0869 116.1738       17 
# Random effects:
#  Groups Name        Std.Dev.
#  site   (Intercept) 0.6059  
# Number of obs: 20, groups:  site, 10
# Fixed Effects:
#        (Intercept)  treatmenttreatment  
#           0.001914            1.824177

Extract results from the binomial GLMM

After running all the models we can extract whatever we are interested in to explore long run behavior. As I was planning this post, I started wondering what the estimate of dispersion would look like from a binomial GLMM that was not over or underdispersed by definition.

With some caveats, which you can read more about in the GLMM FAQ, the sum of the squared Pearson residuals divided by the residual degrees of freedom is an estimate of over/underdispersion. This seems OK to use in the scenario I’ve set up here since my binomial sample sizes are fairly large and my proportions are not too close to the distribution limits.

I made a function to calculate this.

overdisp_fun = function(model) {
     sum( residuals(model, type = "pearson")^2)/df.residual(model)
}
overdisp_fun(mod)
# [1] 0.7169212

Explore estimated dispersion

I want to look at the distribution of dispersion estimates from the 1000 models. This involves looping through the models and using overdisp_fun() to extract the estimated dispersion from each one. I put the result in a data.frame since I’ll be plotting the result with ggplot2. I use purrr helper function map_dfr() for the looping.

alldisp = map_dfr(sims, ~data.frame(disp = overdisp_fun(.x) ) )

Here’s the plot of the resulting distribution. I put a vertical line at 1, since values above 1 indicate overdispersion and below 1 indicate underdispersion.

ggplot(alldisp, aes(x = disp) ) +
     geom_histogram(fill = "blue", 
                    alpha = .25, 
                    bins = 100) +
     geom_vline(xintercept = 1) +
     scale_x_continuous(breaks = seq(0, 2, by = 0.2) ) +
     theme_bw(base_size = 14) +
     labs(x = "Disperson",
          y = "Count")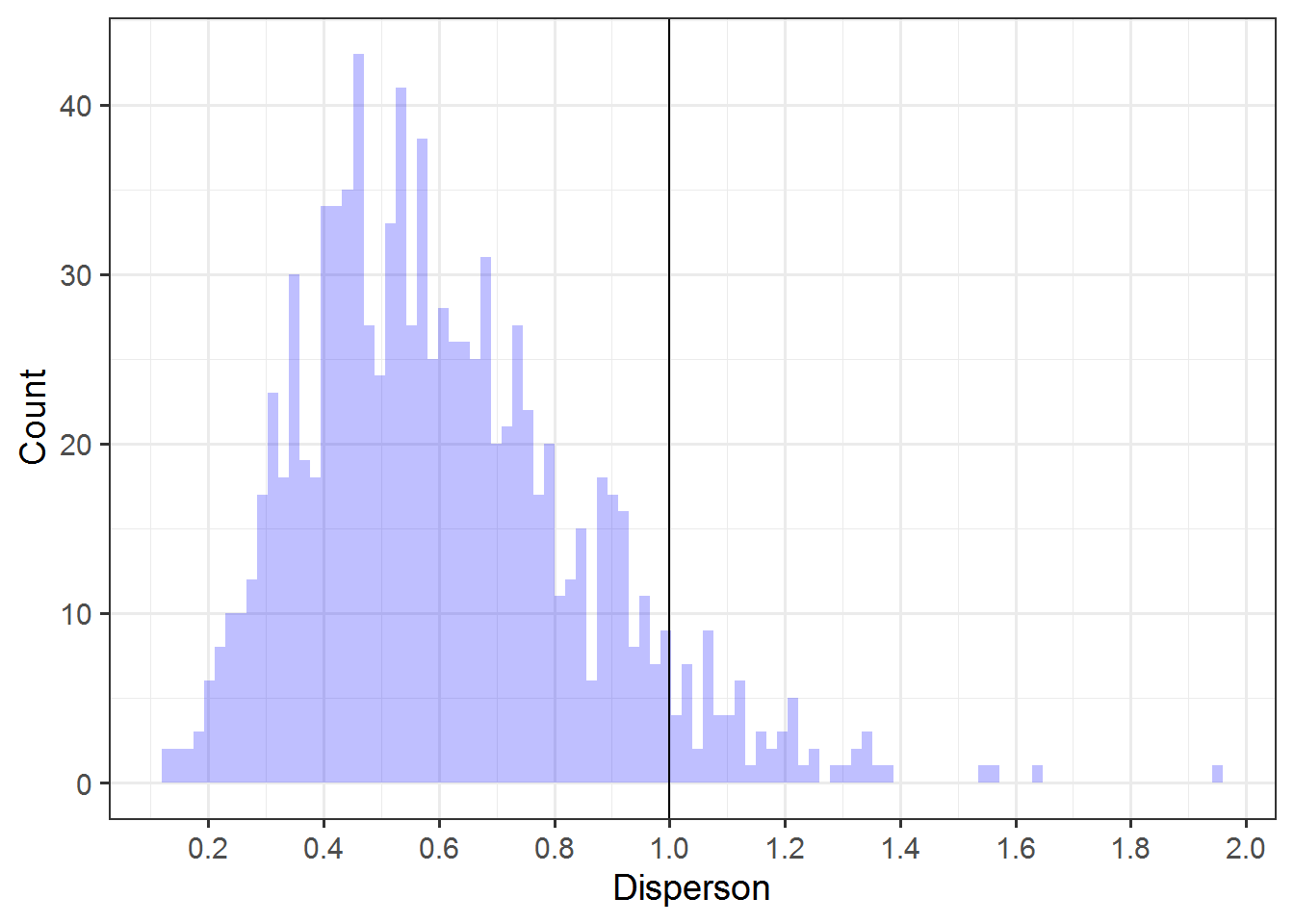

I’m not sure what to think of this yet, but I am pretty fascinated by the result. Only ~7% of models show any overdispersion.

mean(alldisp$disp > 1)
# [1] 0.069

And hardly any (<0.05%) estimate overdispersion greater than 1.5, which is a high enough value that we would likely be concerned that our results were anti-conservative if this were an analysis of a real dataset.

mean(alldisp$disp > 1.5)
# [1] 0.004

For this scenario, at least, I learned that it is rare to observe substantial overdispersion when the model isn’t overdispersed. That seems useful.

I don’t know why so many models show substantial underdispersion, though. Maybe the method for calculating overdispersion doesn’t work well for underdispersion? I’m not sure.

When checking a real model we’d be using additional tools beyond the estimated dispersion to check model fit and decide if a model looks problematic. I highly recommend package DHARMa for checking model fit for GLMM’s (although I’m not necessarily a fan of all the p-values 😜).

Happy simulating!

Just the code, please

Here’s the code without all the discussion. Copy and paste the code below or you can download an R script of uncommented code from here.

library(lme4) # v. 1.1-23
library(purrr) # v. 0.3.4
library(ggplot2) # v. 3.3.2

dat
set.seed(16)
codds = .5/(1 - .5)
todds = .85/(1 - .85)
todds/codds
log(todds/codds)
log(codds)
b0 = 0
b1 = 1.735
site_var = 0.5
n_sites = 10

site = rep(LETTERS[1:n_sites], each = 2)
plot = paste(site, rep(1:2, times = n_sites), sep = "." )
treatment = rep( c("treatment", "control"), times = n_sites)
dat = data.frame(site, plot, treatment)
dat

( site_eff = rep( rnorm(n = n_sites, 
                        mean = 0, 
                        sd = sqrt(site_var) ), 
                  each = 2) )

( log_odds = with(dat, b0 + b1*(treatment == "treatment") + site_eff ) )
( prop = plogis(log_odds) )

dat$num_samp = 50
num_samp = sample(40:50, size = 20, replace = TRUE)
( dat$y = rbinom(n = n_sites*2, size = dat$num_samp, prob = prop) )

mod = glmer(cbind(y, num_samp - y) ~ treatment + (1|site), 
            data = dat,
            family = binomial(link = "logit") )
mod

bin_glmm_fun = function(n_sites = 10,
                        b0 = 0,
                        b1 = 1.735,
                        num_samp = 50,
                        site_var = 0.5) {
     site = rep(LETTERS[1:n_sites], each = 2)
     plot = paste(site, rep(1:2, times = n_sites), sep = "." )
     treatment = rep( c("treatment", "control"), times = n_sites)
     dat = data.frame(site, plot, treatment)           
     
     site_eff = rep( rnorm(n = n_sites, mean = 0, sd = sqrt(site_var) ), each = 2)
     
     log_odds = with(dat, b0 + b1*(treatment == "treatment") + site_eff)
     prop = plogis(log_odds)
     dat$num_samp = num_samp
     dat$y = rbinom(n = n_sites*2, size = num_samp, prob = prop)
     
     glmer(cbind(y, num_samp - y) ~ treatment + (1|site),
           data = dat,
           family = binomial(link = "logit") )
}


set.seed(16)
bin_glmm_fun()

sims = replicate(1000, bin_glmm_fun(), simplify = FALSE )
sims[[100]]

overdisp_fun = function(model) {
     sum( residuals(model, type = "pearson")^2)/df.residual(model)
}
overdisp_fun(mod)

alldisp = map_dfr(sims, ~data.frame(disp = overdisp_fun(.x) ) )

ggplot(alldisp, aes(x = disp) ) +
     geom_histogram(fill = "blue", 
                    alpha = .25, 
                    bins = 100) +
     geom_vline(xintercept = 1) +
     scale_x_continuous(breaks = seq(0, 2, by = 0.2) ) +
     theme_bw(base_size = 14) +
     labs(x = "Disperson",
          y = "Count")

mean(alldisp$disp > 1)
mean(alldisp$disp > 1.5)